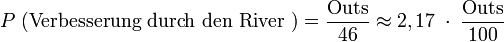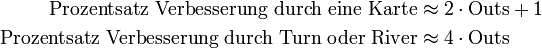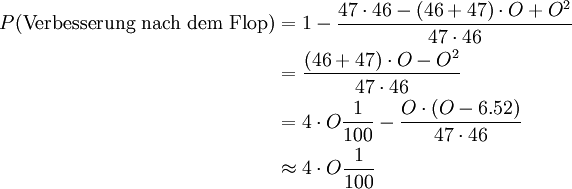Berechnung von Outs und Odds
Als Outs bezeichnet man die Anzahl der zur Verbesserung der aktuellen Hand fähigen Karten, um eine gewinnfähige Hand zu bekommen.
Hat man zum Beispiel auf der Hand A♥ K♥ und auf dem Flop liegen 3♠ 5♥ 7♥, so benötigt man eine weitere Herzkarte, um aus dem Flush Draw einen vollständigen Flush zu machen. Im gesamten Spiel befinden sich 13 Karten mit der Farbe Herz. Vier davon (zwei auf der Hand, zwei auf dem Board) liegen bereits. Die restlichen neun Herzkarten sind nun die Outs.
Als Odds bezeichnet man die Wahrscheinlichkeit, eine der fehlenden out-Karten zu bekommen.
Da man seine Hole Cards und den Flop kennt, bleiben nach dem Flop von ehemals 52 noch 47 Karten übrig, in denen die Outs enthalten sind.
Die Wahrscheinlichkeit, seine Karten durch die Turn Karte zu verbessern, sind:
Ist der Turn auf dem Tisch, so sind noch 46 Karten unbekannt. Damit gilt für die Wahrscheinlichkeit, seine Karten durch die River-Karte zu verbessern, fast das gleiche:
Aus der Anzahl der outs kann man mit der sogenannten Faustregel die Wahrscheinlichkeit in Prozent bestimmen, diese outs zu bekommen:
Da vor allem Wahrscheinlichkeiten mit ca. 8 Outs interessant sind ist die erste Formel eine gute Näherung sowohl nach der Turn als auch nach der River Karte. Die Wahrscheinlichkeiten für eine Verbesserung durch die Turn- oder Riverkarte werden später hergeleitet. Folgende Tabelle gibt aber schon einen Überblick der Faustregeln zu den im Poker besonders interessanten Händen:
Wichtige Wahrscheinlichkeiten für Verbesserung nach dem Flop/Turn [
| Aktuelle Hand | Outs | Wahrscheinlichkeit Turn + River Faustregel |
Wahrscheinlichkeit Turn + River mathematisch exakt |
Wahrscheinlichkeit River Faustregel |
Wahrscheinlichkeit River mathematisch exakt |
|---|---|---|---|---|---|
| Flush Draw z.B.A♥ K♥ Flop:3♠ 5♥ 7♥ |
9 2♥ 3♥4♥6♥8♥ 9♥ 10♥B♥D♥ |
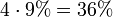 |
34,97 % | 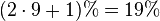 |
19,57 % |
| Open Ended Straight Draw z.B.10♥ B♣ Flop:8♠ 9♦ 2♥ |
8 7♦7♥7♠7♣ D♦D♥D♠D♣ |
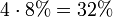 |
31,45 % | 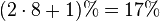 |
17,39 % |
| Doppelter Gutshot z.B.10♥ D♣ Flop:6♠ 8♦ 9♥ |
8 7♦7♥7♠7♣ B♦B♥B♠B♣ |
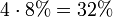 |
31,45 % | 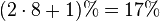 |
17,39 % |
| Gutshot z.B.10♥ D♣ Flop:5♠ 8♦ 9♥ |
4 B♦B♥B♠B♣ |
 |
16,47 % | 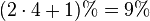 |
8,70 % |
| Flush Draw + Open Ended Straight Draw z.B.10♥ B♥ Flop:8♠ 9♥ 4♥ |
15 = 9 + 8 - 2 2♥3♥5♥6♥7♥8♥ D♥ K♥A♥ 7♦7♠7♣ D♦D♠D♣ |
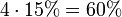 |
54,12 % | 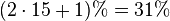 |
32,61 % |
Bei kombinierten Karten wie einem Flush Draw und einem Open Ended Straight Draw darf man die Karten, die beide Draws verbessern, nur einfach zählen. In unserem Beispiel verbessert die 7♥ und die D♥ sowohl den Flush als auch den Open Ended Straight Draw. Man hat also nicht 17 Outs, die man erhält, wenn man die neun vom Flush Draw plus acht vom Open Ended Straight Draw addiert. Bei vielen Outs erhält man mit der Faustregel für den Turn oder River (eine Karte) eine zu hohe (kleine) Prozentzahl.
Die Wahrscheinlichkeit für eine Verbesserung durch die Turn- oder River-Karte erhält man über das Gegenereignis. Man berechnet also die Wahrscheinlichkeit, dass sowohl am Turn als auch am River keine der Outs (wir bezeichnen sie hier mit O) zu sehen sind:
47 Karten sind nach dem Flop noch unbekannt, 47 − O Karten verbessern die Hand nicht. Nach dem Turn sind nur noch 46 Karten unbekannt, davon verbessern 46 − O Karten die Hand nicht. Die Wahrscheinlichkeit, seine Karten am Turn oder River zu verbessern, ist also:
Nachdem man die Wahrscheinlichkeit bestimmt hat, gegen eine beim Gegner vermutete Hand wie etwa Top Pair Top Kicker zu gewinnen, muss man dies noch gegen den zu zahlenden Einsatz, relativ zum zu erzielenden Gewinn, setzen, um zu bestimmen, ob sich der Einsatz lohnt.